Richard Vasques, Rachel Slaybaugh
This work studies mathematical models for more accurately performing neutral particle transport in certain physical regimes. In classical particle transport, the scattering centers in the background material are assumed to be Poisson-distributed; that is, their spatial locations are uncorrelated. When this is true, the probability that a particle interacts with the background medium is proportional to the path length traveled by that particle, with the proportionality constant depending on the density of the medium and on the particle’s energy. This leads to an exponential attenuation law, with the particle flux decreasing as an exponential function of the path length (Beer-Lambert law).
However, in certain inhomogeneous random media in which the locations of the scattering centers are spatially correlated, the particle flux will experience a non-exponential attenuation law that is not captured by classical homogenization techniques. A nonclassical theory for this type of transport problem has been recently introduced, proposing a homogenization that preserves the path length distribution for particles traveling in the inhomogeneous medium. This new approach has sparked a vivid discussion in the recent literature.
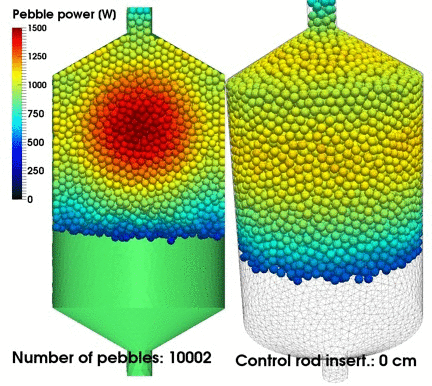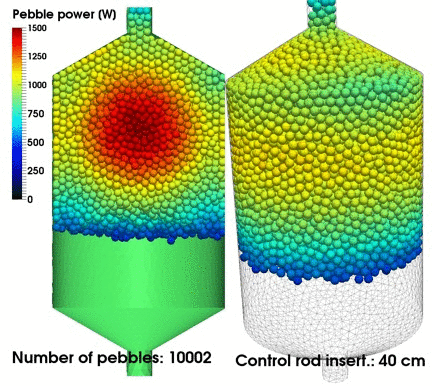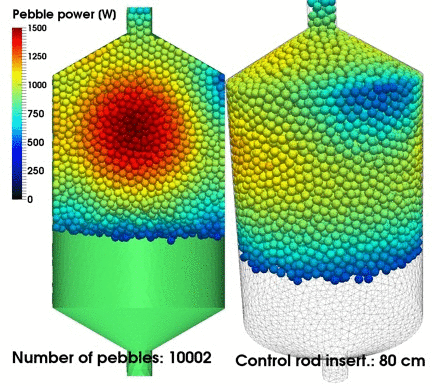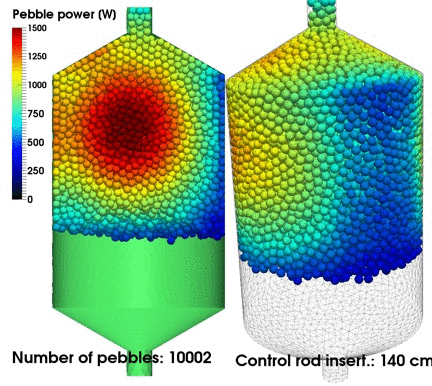
Important applications for this non-classical theory include neutron transport in Pebble Bed Reactors (in which a non-exponential path-length distribution arises due to the pebble arrangement within the core) and photon transport in atmospheric clouds (in which the locations of the water droplets in the cloud seem to be correlated in ways that measurably affect the radiative transfer within the cloud).