Category: Research

A nonstiff solution for the stochastic neutron point kinetics equations

Introducing an approach that yields a nonstiff solution to solve the stochastic neutron point kinetics equations.

Title

A nonstiff solution for the stochastic neutron point kinetics equations

Author(s)

Milena Wollmann da Silva, Richard Vasques, Bardo E.J. Bodmann, Marco T. Vilhena

Publication

Annals of Nuclear Energy 97: 47-52

Description

We propose an approach to solve the stochastic neutron point kinetics equations using an adaptation of the diagonalization-decomposition method (DDM). This new approach (Double-DDM) yields a nonstiff solution for the stochastic formulation, allowing the calculation of the neutron and precursor densities at any time of interest without the need of using progressive time steps. We use Double-DDM to compute results for stochastic problems with constant, linear, and sinusoidal reactivities. We show that these results strongly agree with those obtained by other approaches established in the literature. We also compute and analyze the first four statistical moments of the solutions.

Link to Publication

Nonclassical particle transport in the 1-D diffusive limit

We provide computational results demonstrating for the first time that the solution of the nonclassical particle transport equation is well-approximated
by the solution of the nonclassical diffusion equation.

Title

Nonclassical particle transport in the 1-D diffusive limit

Author(s)

Richard Vasques, Rachel N. Slaybaugh, Kai Krycki

Publication

Transactions of the American Nuclear Society 114: 361-364

Description

In this paper, we investigate nonclassical particle transport taking place in a 1-D random periodic diffusive system. We provide computational results that validate the theoretical predictions, demonstrating for the first time that the solution of the nonclassical particle transport equation is well-approximated
by the solution of the nonclassical diffusion equation.

Link to Publication

The nonclassical diffusion approximation to the nonclassical linear Boltzmann equation

Showing that the nonclassical diffusion equation can be represented exactly by the nonclassical linear Boltzmann equation for an infinite homogeneous medium.

Title

The nonclassical diffusion approximation to the nonclassical linear Boltzmann equation

Author(s)

Richard Vasques*

Publication

Applied Mathematics Letters 53: 63–68

Description

We show that, by correctly selecting the probability distribution function for a particle’s distance-to-collision, the nonclassical diffusion equation can be represented exactly by the nonclassical linear Boltzmann equation for an infinite homogeneous medium. This choice of probability distribution function preserves the true mean-squared free path of the system.

Link to Publication

MocDown

Jeffrey Seifried (alumnus)

MocDown (http://jeffseif.github.io/MocDown/) is an efficient tool which loosely couples simulations for neutron transport, isotopic transmutation, thermo-fluids, and the equilibrium core composition search within advanced nuclear reactor cores. The development of MocDown focused on facilitating both fast runtime (by employing concurrent threading and efficient regex parsing when possible) and fast post-processing (with simple and consistent hierarchical storage of result files). MocDown also employs object-oriented programming in Python 3 for flexible modification with external libraries.

To do so, MocDown couples three models for self-consistent simulations: thermo-fluids, neutron transport, and transmutation and recycling. The MocDown accelerated recycling scheme efficiently finds the equilibrium cycle, whose isotopic composition matches that of its successor. Using these techniques, MocDown has been successfully used to simulate the RBWR-Th design, a fuel-self-sustaining nuclear reactor core design which operates with only thorium as its charge.

Adjoint-based uncertainty quantification in multiphysics reactor modeling

Manuele Aufiero, Michael Martin, Massimiliano Fratoni

Coupled neutronics-thermal/hydraulics simulations are of great interest for the analysis and design of nuclear reactors. Ongoing studies of advanced and GEN-IV reactors call for the adoption of accurate modeling tools that are based on Monte Carlo neutron transport and CFD-based T/H solutions. In this framework, the capability to propagate uncertainties in the input data through the coupled simulation is highly desirable.

Recently, Generalized Perturbation Theory (GPT) methods have been implemented in continuous energy Monte Carlo codes, broadly expanding their capabilities. Some of these methods (e.g., available in the Serpent code) are suitable to be adopted in combination with Open Source finite-volume libraries for continuum mechanics solvers (e.g., the OpenFOAM C++ multiphysics toolkit).

The present project involves the projection of the input uncertainties and the reactor generalized responses onto sets of orthogonal basis functions, along with the adoption of extended GPT methods for the calculation of sensitivities in the coupled problems. The comparison of nuclear data uncertainty propagation results against standard methods in simple benchmark cases shows that the new approach might provide a reliable and efficient option for Uncertainty Quantification in multiphysics problems.

Sensitivity and uncertainty analysis in Monte Carlo transport and burnup calculations

Yishu Qiu, Manuele Aufiero, Kan Wang (Tsinghua University), Massimiliano Fratoni

f28f25 comparisonThere is an increasing interest to couple Monte Carlo (MC) transport calculations to depletion/burnup codes since Monte Carlo codes can provide exact flux distributions or cross sections. One of the main concerns about using a MC transport-depletion method is how uncertainties from Monte Carlo statistical uncertainties as well as nuclear data uncertainties are be propagated between the Monte Carlo codes and burnup codes. This project is going to develop sensitivity and uncertainty analysis capabilities in RMC-Depth which is an in-coupling Monte Carlo transport-depletion code developed by Tsinghua University, China. To be more specific, the goals of this project are:
1. Study methods suitable for computing k-eigenvalue sensitivity coefficients with regard to the continuous-energy cross sections and implement them in RMC; conduct sensitivity and uncertainty analysis of the effective multiplication factor to nuclear data uncertainties in the transport calculations.
2. Study methods appropriate for computing general response sensitivity coefficients with regard to the continuous-energy cross sections and implement them in RMC; conduct sensitivity and uncertainty analysis of general responses in the form of linear response functions, such as relative powers, isotope conversion ratios, multi-group cross sections, and bilinear response functions, such as adjoint-weighted kinetic parameters, to nuclear data in the transport calculations.
3. Study the methods suitable for analysis and uncertainty propagation in Monte Carlo transport-burnup calculations. With the proposed methods, propagate uncertainties in the Monte Carlo transport-burnup calculations that come from nuclear data, the Monte Carlo statistics, the isotope number densities, and the cross-correlations between the nuclear data and the number densities. These effects should be analyzed separately in each burnup step of the burnup calculations.
4. Study the methods suitable for uncertainty qualifications for other parameters such as temperature and system dimensions.

PyNE

Josh Howland, Marissa Ramirez-Zweiger (alumna), Katy Huff, Rachel Slaybaugh

Tools used in the fields of Data and Computational Science have undergone many rapid modernizations, including a shift to the use of cleaner, more forgiving programming languages and frameworks. Computational neutronics has begun to follow this trend, though this is impeded by the number of legacy codes are written in older, less accessible languages and under antiquated programming modes. Recent work in PyNE aims enable the transition to modern languages and programming paradigms, providing modules in Python that interface with legacy Fortran programs.

The National Nuclear Data Center (NNDC) provides a suite of Evaluated Nuclear Structure Data File (ENSDF) Analysis and Utility programs written in Fortran.  Constantly trying to manage and call 20+ different executables is hard to manage and can rapidly become fragmented. Work is in progress to create a Python interface for the majority of these programs in PyNE.  Python allows for significantly easier access, and modern paradigms in programming including testing and modularity.   

Non-Classical Transport Methods

Richard Vasques, Rachel Slaybaugh

This work studies mathematical models for more accurately performing neutral particle transport in certain physical regimes. In classical particle transport, the scattering centers in the background material are assumed to be Poisson-distributed; that is, their spatial locations are uncorrelated. When this is true, the probability that a particle interacts with the background medium is proportional to the path length traveled by that particle, with the proportionality constant depending on the density of the medium and on the particle’s energy. This leads to an exponential attenuation law, with the particle flux decreasing as an exponential function of the path length (Beer-Lambert law).

However, in certain inhomogeneous random media in which the locations of the scattering centers are spatially correlated, the particle flux will experience a non-exponential attenuation law that is not captured by classical homogenization techniques. A nonclassical theory for this type of transport problem has been recently introduced, proposing a homogenization that preserves the path length distribution for particles traveling in the inhomogeneous medium. This new approach has sparked a vivid discussion in the recent literature.

Important applications for this non-classical theory include neutron transport in Pebble Bed Reactors (in which a non-exponential path-length distribution arises due to the pebble arrangement within the core) and photon transport in atmospheric clouds (in which the locations of the water droplets in the cloud seem to be correlated in ways that measurably affect the radiative transfer within the cloud).

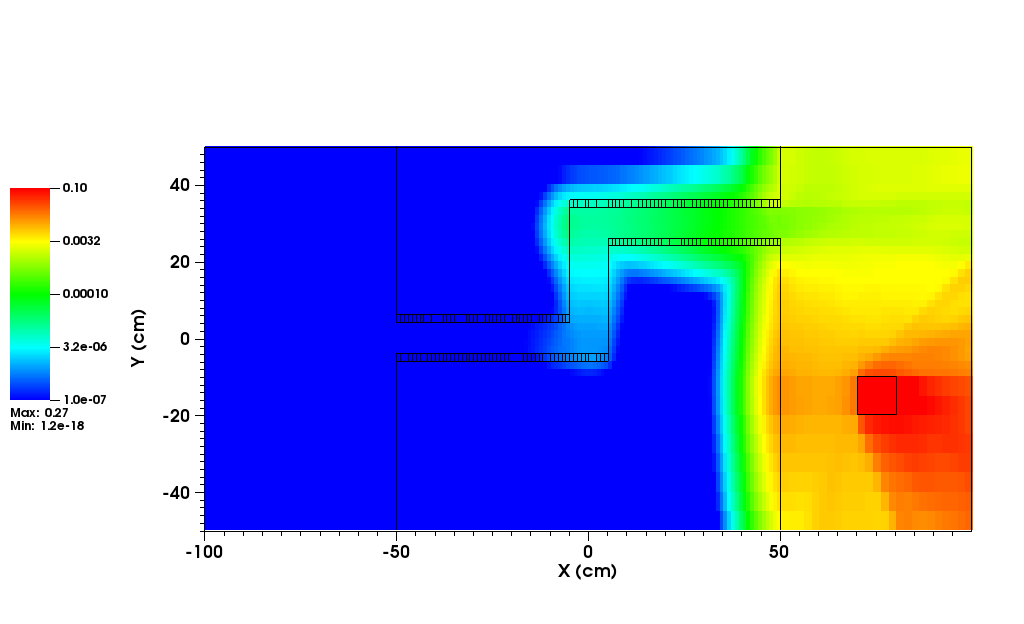
Angle-Informed Hybrid Methods

Madicken Munk, Garrett Baltz, Rachel Slaybaugh, Richard Vasques

Hybrid methods for radiation transport aim to use the speed and uniform uncertainty distribution obtained from deterministic transport to accelerate and improve performance in Monte Carlo transport. An effective use of this type of transport hybridization can lead to a reduced uncertainty in the solution and/or a faster time to a solution. However, not all hybrid methods work for all types of radiation transport problems. In problems where the method is not well-suited for the problem physics, a hybrid method may perform more poorly than analog Monte Carlo, leading to wasted computer time and energy, or even no acceptable solution.

This project builds on existing software infrastructure (ORNL’s Denovo and ADVANTG) to generate hybrid methods for deep-penetration radiation transport problems. Specifically, we are developing variance reduction parameters for problems with strong angular anisotropy without explicitly including angular biasing parameters. No existing, highly accessible, automated hybrid method has incorporated angular-dependence of the flux in generating variance reduction parameters, which has led to difficulty in the analysis of highly anisotropic problems. Our method should improve the computational performance of hybrid methods for anisotropic problems while also maintaining similar space and processing metrics as energy- and space- exclusive hybrid methods.

Molten salt reactors modeling and analysis

Daniel Wooten, Manuele Aufiero, Francesco Accardi, Massimiliano Fratoni

Molten salt reactors, those reactors whose coolant or fuel is a molten salt (for example, table salt melts around 1440F), have gained increased national and international attention in the past decade because of their inherent safety, lack of pressurized systems (reduced cost), and high fuel utilization. A handful of molten salt reactors have been built; most notably the MSRE at Oak Ridge National Laboratory in the 1960’s.

Despite the long, uneventful, and largely successful operation of the MSRE, molten salt reactors fell out of political favor and little development has occurred with regards to the technology since. Currently, this group’s focus is on the development of computational methods to bring modern nuclear analysis tools to bear on the investigation of hypothetical molten salt reactors. These tools are used to learn about the likely behavior of such reactors and allow for their neutronic, safety, and economic analysis.